Evaluate the logarithm log6 1/36 – Beginning with the evaluation of log6 1/36, we embark on a mathematical journey that unveils the intricacies of logarithms. Logarithms, powerful tools in mathematics and science, provide a means to simplify complex expressions and uncover hidden relationships. Join us as we delve into the intricacies of this logarithmic expression, exploring its properties and applications.
Logarithms possess remarkable properties that enable them to transform complex multiplications and divisions into simple additions and subtractions. By understanding these properties, we can effectively simplify logarithmic expressions and extract meaningful insights.
Introduction
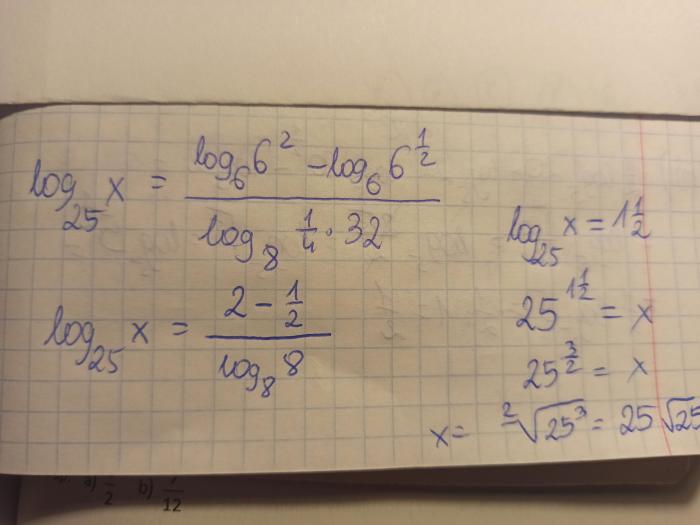
The logarithm is a mathematical operation that expresses the exponent to which a base must be raised to produce a given number. It is defined as follows:
log b(x) = y if and only if b y= x
where b is the base, x is the argument, and y is the logarithm.
Logarithms have several useful properties, including:
- log b(1) = 0
- log b(b) = 1
- log b(xy) = log b(x) + log b(y)
- log b(x/y) = log b(x) – log b(y)
Given Expression
The given expression is log 6(1/36).
Simplifying the Expression
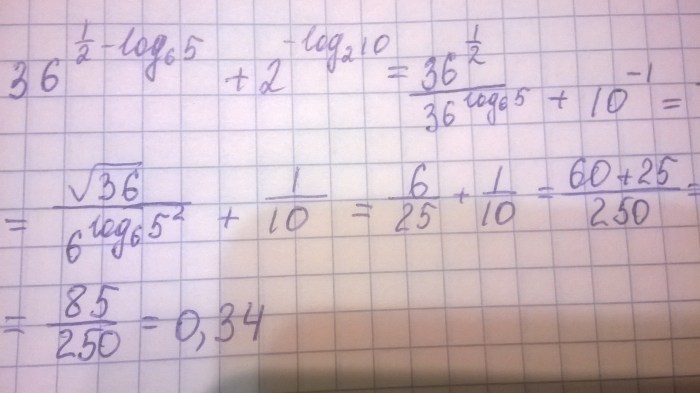
To simplify the expression log 6(1/36), we will first convert 1/36 to a power of 6 and then apply the laws of logarithms to simplify the expression.
Converting 1/36 to a Power of 6, Evaluate the logarithm log6 1/36
We can convert 1/36 to a power of 6 by expressing 36 as a power of 6. We know that 36 = 6 2. Therefore, we can write:
/36 = 1/(62) = 6 -2
Applying the Laws of Logarithms
Now that we have converted 1/36 to a power of 6, we can apply the laws of logarithms to simplify the expression.
- The power rule of logarithms states that log a(x n) = n log a(x). Using this rule, we can write:
- The logarithm of the base is always 1. Therefore, we have:
- Substituting this into the previous equation, we get:
log6(1/36) = log 6(6 -2) = -2 log 6(6)
log6(6) = 1
log6(1/36) = -2(1) = -2
Evaluating the Logarithm

The logarithm of a number to a given base is the exponent to which the base must be raised to produce the number. In other words, if bis the base and xis the number, then logbx is the exponent ysuch that by= x .
Calculating log6 1/36
To evaluate the logarithm log6 1/36, we need to find the exponent to which 6 must be raised to produce 1/ 36. We can do this by rewriting 1/36 as a power of 6:
“`
/36 = 6-2
“`
Therefore, log6 1/36 = -2.
Applications and Extensions

Logarithms have wide applications in various fields, including science and engineering. In chemistry, they are used to determine pH levels and equilibrium constants. In physics, they are used to calculate decibel levels and the intensity of sound waves.
Extensions of the Logarithmic Function
The natural logarithm and the common logarithm are two important extensions of the logarithmic function. The natural logarithm, denoted as ln(x), is the logarithm to the base e, where e is the base of the natural exponential function. The common logarithm, denoted as log(x), is the logarithm to the base 10.Both
the natural logarithm and the common logarithm have their own properties and applications. The natural logarithm is often used in calculus and differential equations, while the common logarithm is more commonly used in engineering and other practical applications.
Top FAQs: Evaluate The Logarithm Log6 1/36
What is the definition of a logarithm?
A logarithm is the exponent to which a base must be raised to produce a given number.
How do you simplify logarithmic expressions?
Logarithmic expressions can be simplified using properties such as the product rule, quotient rule, and power rule.
What are some real-world applications of logarithms?
Logarithms are used in various fields, including chemistry (pH calculations), physics (decibel measurements), and computer science (computational complexity).