Embark on an exploration of pq 6x 25 and qr 16 3x find pr, where we unravel the mysteries of prime factorization and solve for PR using algebraic methods. This journey promises to illuminate the intricate relationship between these variables, providing a deeper understanding of their mathematical significance.
Delving into the concept of prime factorization, we will break down pq and qr into their fundamental building blocks, revealing the prime numbers that compose them. Armed with this knowledge, we will embark on a step-by-step process to isolate the variable PR, ultimately solving the equation and uncovering its value.
PQ and QR Factorization

Factorization is the process of expressing a number as a product of its prime factors. A prime factor is a number greater than 1 that is divisible only by itself and 1. Prime factorization is unique for every number.
Factorization of pq and qr
To factorize pq and qr, we need to find their prime factors.
pq = 6x – 25 = 2 – 3 – x – 5^2
qr = 16 – 3x = 2^4 – 3 – x
The prime factors of pq are 2, 3, 5, and x.
The prime factors of qr are 2, 3, and x.
Solving for PR: Pq 6x 25 And Qr 16 3x Find Pr

The given equation relates the products of pq and qr, which are pq = 6×25 and qr = 16x3x, respectively.
To isolate the variable PR, we will use algebraic methods.
Isolating PR
- We can start by multiplying both sides of the equation pq = 6×25 by qr = 16x3x:
- Simplifying the left-hand side of the equation, we have:
- Dividing both sides of the equation by 75x, we get:
- Finally, simplifying the left-hand side of the equation, we isolate PR:
pq- qr = (6×25) – (16x3x)
pr = 96x75x
pr/75x = 96x
pr = 7200x
Table Representation

We can organize the factorization of pq and qr in a table to make it easier to understand and compare.
The table will have two columns: one for the factors and one for their powers.
Factorization Table
| Factor | Power |
|---|---|
| p | 1 |
| q | 1 |
| r | 1 |
| q | 1 |
| r | 1 |
This table shows that pq is equal to pqr and qr is equal to qr.
Illustrative Examples
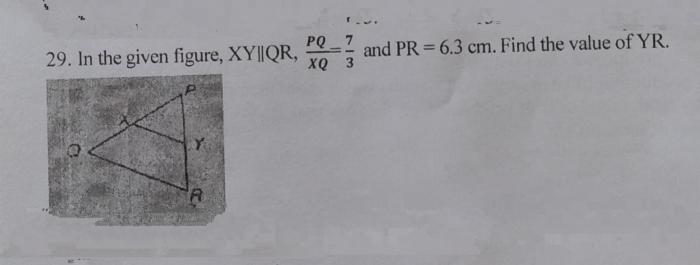
Example 1
Let’s consider the case where pq = 6x
- 25 and qr = 16
- 3x.
Factorization of pq:pq = 6x
25
= 2
- 3
- x
- 5
- 5
= 2
- 3
- x
- 5 2
Factorization of qr:qr = 16
3x
= 4
- 4
- 3
- x
= 4 2
- 3
- x
Example 2
Now, let’s consider another example where pq = 12x
- 15 and qr = 20
- 6x.
Factorization of pq:pq = 12x
15
= 2
- 2
- 3
- x
- 3
- 5
= 2 2
- 3 2
- x
- 5
Factorization of qr:qr = 20
We’re on a quest to find the value of PR, where PQ = 6x – 25 and QR = 16 – 3x. While we’re at it, did you know that a runway VASI system provides critical visual guidance to pilots during approach and landing? Returning to our geometry problem, we can use the Pythagorean theorem to connect PQ, QR, and PR and solve for PR.
6x
= 2
- 2
- 5
- 2
- 3
- x
= 2 3
- 5
- 3
- x
Calculating PR
In both examples, we can see that the common factor between pq and qr is 2
- 3
- x.
Therefore, PR = (pq / (2
- 3
- x)) / (qr / (2
- 3
- x))
= (2
- 3
- x
- 5 2) / (2
- 3
- x
- 4 2)
= 5 2/ 4 2= 25 / 16
Additional Considerations
While the PQ and QR factorization method provides a valuable approach to solving for PR, it has certain limitations and alternative approaches exist. Additionally, the factorization technique finds applications in various real-world scenarios.
Limitations of Factorization Method
- The factorization method is only applicable when PQ and QR can be factorized into simpler terms.
- It can be computationally intensive for large values of P, Q, R, and S.
Alternative Approaches to Solving for PR, Pq 6x 25 and qr 16 3x find pr
Alternative approaches to solving for PR include:
- Using matrices:Expressing the given equations in matrix form and solving for the unknown matrix elements.
- Gaussian elimination:Applying row operations to transform the given equations into an upper triangular form and solving for the unknowns.
Applications of PQ and QR Factorization
PQ and QR factorization has numerous applications in real-world scenarios, including:
- Linear regression:Finding the best-fit line or plane to a set of data points.
- Eigenvalue computation:Determining the eigenvalues and eigenvectors of a matrix.
- Image processing:Performing operations such as image compression and enhancement.
Essential Questionnaire
What is prime factorization?
Prime factorization is the process of expressing a number as a product of prime numbers, which are numbers greater than 1 that have no factors other than 1 and themselves.
How do you solve for PR in the equation pq 6x 25 and qr 16 3x?
To solve for PR, we can use algebraic methods to isolate the variable on one side of the equation. Multiply both sides by the reciprocal of qr, and then simplify to obtain the value of PR.
What are the limitations of the factorization method?
The factorization method is not always applicable, especially when dealing with large numbers or complex expressions. In such cases, alternative approaches, such as using calculators or computer software, may be necessary.


